arctan(1.76)。

定义。

arctan(1.76)反切函数的结果，该函数返回一个角度，其正切值为1.76。它可以写成：。

arctan(1.76)=θ。

其中θ以弧度表示的角度。

计算结果。

使用计算器或数学软件可以计算arctan(1.76)：。

θ≈62.13°。

这表示角度约为62.13度。

几何意义。

arctan(1.76)可以用直角三角形来解释。设有一个直角三角形，其中一个直角相邻边长为1，对边长为1.76。arctan(1.76)这个三角形的锐角，也就是以相邻边为底边的角。

应用。

arctan(1.76)在许多领域都有应用，包括：。

三角学：计算三角形中缺失的角度。

微积分：求导数和积分。

物理学：描述运动和振荡。

工程：设计桥梁、建筑物和其他结构。

arctan怎么化成tan

arcta怎么化成ta？

arcta的定义

arcta（反正切）函数是切线函数的逆函数，它将一个角度或斜率值映射到介于-π/2和π/2之间的角度。

化成ta公式

要将arcta化成ta，可以使用以下公式：

ta(arcta(x))=x

证明

证明这个公式很简单，利用ta和arcta的定义：

ta(arcta(x))=ta(θ)

其中θ=arcta(x)

则x=ta(θ)

所以ta(arcta(x))=x

示例

例如，要将arcta(-0.5)化成ta，我们可以使用公式：

ta(arcta(-0.5))=-0.5

结论

通过使用ta(arcta(x))=x公式，我们可以轻松地将arcta化成ta。这在数学和工程应用中很有用，其中需要将角度或斜率值相互转换。

arctan特殊值对照表

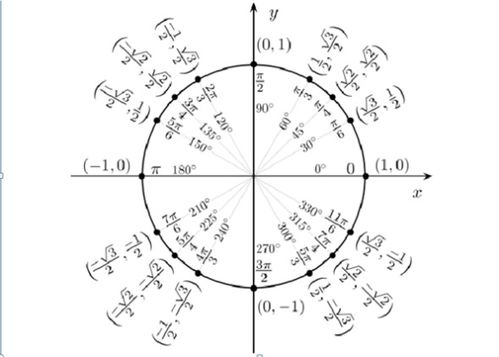
arcta特殊值对照表

arcta函数，也被称为反切函数，是三角函数的一种，用于求取给定正切值对应的角度。在某些特殊情况下，arcta函数有特定的值，形成对照表，便于快速查阅。

arcta特殊值

以下是对照表中包含的arcta特殊值：

arcta(0)=0

arcta(1)=π/4

arcta(-1)=-π/4

arcta(∞)=π/2

arcta(-∞)=-π/2

arcta特殊值对照表

下表总结了上述arcta特殊值：

参数

值

0

0

1

π/4

-1

-π/4

∞

π/2

-∞

-π/2

标签：arcta，反切函数，特殊值对照表

arctan负∞为多少

arcta(-∞)的值是多少？

arcta定义

反正切函数（arcta）是切线函数的逆函数。其定义域为实数集，值域为(-π/2,π/2)。arcta(-x)=-arcta(x)。

arcta(-∞)的值

当x趋于负无穷大时，切线函数ta(x)也会趋于负无穷大。因此，反正切函数arcta(-∞)的值等于-π/2。

应用

arcta(-∞)在数学和科学中有多种应用，包括：

三角函数的求值

积分的计算

复分析中的复数角论证

总结

因此，arcta(-∞)=-π/2。这个值是通过考虑切线函数的极限行为得出的。arcta(-∞)在数学和科学中有着广泛的应用，对于理解三角函数和复数角论证至关重要。

标签：

arcta,无穷大,三角函数,反正切