2.76减1.76等于几目录
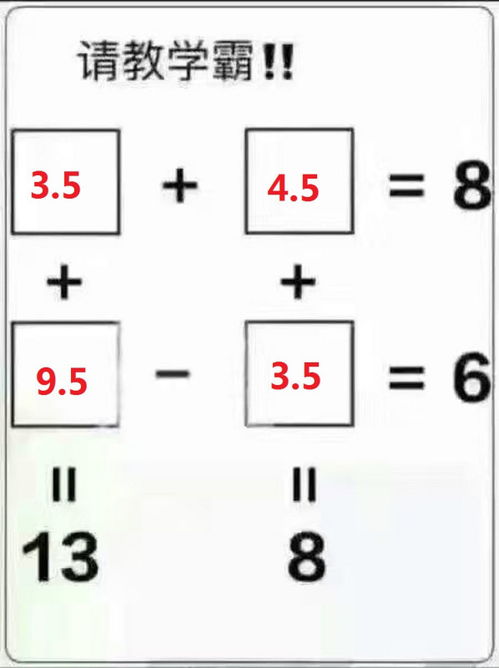
2.76减去1.76就是1.00。

3*引言
乘法是数学的基本计算方法,可以快速计算两个或多个数字相乘的结果。今天讨论具体的乘法问题。260乘30多少钱?在这篇文章中,我想详细解答这个问题,并思考乘法在日常生活和数学学习中的重要性。
3
乘法的基本概念。
乘法是表示加法的重复的运算。例如,3乘4可以理解为4加3次,也就是4 4 4。数学中,乘法通常用“×”这个符号来表示。乘法有交换律和结合律。也就是说,a乘以b等于b乘以a,(a乘以b)乘以c等于a(b乘以c)。
3
260乘以30。
要计算260乘以30,你可以用长乘法,也可以直接用计算器。这里用长乘法表来展示具体的计算步骤。
首先,将30乘以3分解为10。这样一来,就可以把问题分解成两个更简单的乘法问题。260乘以3和260乘以10。
1.计算260乘以3。
260
×3
------
780
2.计算260乘以10。
260
×10。
------
2600
然后将两个结果相加,得出最终答案。
780
2600。
------
3380
因此,260乘30等于3380。
3
乘法在日常生活中的应用。
乘法在日常生活中被广泛使用。下面是一些常见的例子。
以30元购买3件商品为例,合计价格为3×30,即90元。
在烹饪时计算食材的量。如果需要将食材的量增加一倍,可以使用乘法来计算新的量。
面积和体积计算:在建筑和工程领域,乘法用于面积和体积计算,这对于确保项目的准确性非常重要。
3
乘法在数学学习中的重要性
乘法是数学学习的基础之一。掌握乘法可以帮助你更好地理解分数、百分比、代数等数学上的其他概念。下面介绍一些乘法在数学学习中的重要性:
提高计算能力:乘法是提高计算速度和准确性的关键。
理解数学概念。乘法是理解分数,百分比,代数等概念的基础。
逻辑思维的培养:通过解答乘法问题,可以培养学生的逻辑思维和解决问题的能力。
3
结论。
260×30等于3380。这是一个简单的乘法问题,但在数学和日常生活中有重要应用。通过学习和掌握乘法,可以提高计算能力,理解数学概念,解决实际生活中的问题。因此,乘法是数学学习的重要组成部分,值得深入学习和掌握。

3*引言
在数学中,根是一个非常重要的概念。数的平方根。是用某个数乘以自己原来的数。例如,2乘2等于4,所以4的平方根是2。这里考察4的平方根√2,详细说明其数值和意义。
3
√2是什么?
√2是表示2的平方根的无理数。也就是说不存在正确表示√2的整数或分数这是无限不循环小数,前面的小数是1.41421356237…是。
3
√2的发现和历史。
√2的概念可以追溯到古代数学家。古希腊开始研究包括√2在内的无理数。传说,古希腊数学家毕达哥拉斯发现了直角三角形的两个直角边的平方和等于斜边的平方的定理。这个定理后来被称为毕达哥拉斯定理,√2就是从这个定理中诞生的。
3
√2的数值特性。
√2是无理数,但可以用数学方法近似。例如,你可以使用牛顿迭代法来近似√2的值。用这种方法,你可以不断提高近似值的精度,直到达到你需要的精度。
3
√2数学应用。
√2在数学中被广泛使用。以下是一些例子
几何学:在几何学中,√2经常出现在各种几何图形的边长和面积的计算中。
三角法:在三角法中,√2与正弦、余弦、正切等三角函数有关。
在微积分中√2可以出现在微积分的计算中。
3
√2的近似值
√2是无理数,所以不能得到准确的值。但是,近似值可以通过计算确定。以下是一些常见的近似值:
3.14(π的近似值)
1.414(四舍五入到小数点以下三位)
1.41421(四舍五入到小数点后五位)
3
√2的数学证明。
√2是无理数。这意味着它不能表示为两个整数的比值。下面是√2是一个无理数的简单证明。
有理数√2可以表示为两个整数的比值。√2=a/b,a和b是互质整数。
将这个方程式的两边平方,得到2=a^2/b^2。
这两条边乘以b^2,得到2b^2=a^2。
这意味着a^2是2的倍数。因此,a也是2的倍数。
假设a=2c。其中c是整数。将a=2c代入2b^2=a^2,则2b^2=(2c)^2。也就是2b^2=4c^2。
这两条边都除以2,得到b^2=c^2。
这意味着b^2也是2的倍数。因此b也是2的倍数。
这与假设a和b互质相矛盾,所以√2不能表示为两个整数之比,也就是无理数。
3
结论。
√2是无理数,在数学中被广泛使用。虽然不能得到正确的值,但是可以通过计算得到近似值。在这篇文章中,我想让大家加深对√2的理解。
标签:数学,平方根,√2,无理数,毕达哥拉斯定理。

3*引言
在数学世界中,乘法是一种基本的计算方法,实际上可以帮助解决各种问题。今天讨论一个特定的乘法问题。几乘几等于176。这个问题不仅考验你的数学能力,还能激发你对数字组合的好奇心。
3
问题分析。
要找到等于176的两个数,可以通过分解176的因数来解决这个问题。首先,我们需要知道176的因数。
3
因数分解。
176的因数分解如下。
176=1×6
176=2×8
176=4×4
176=8×22
176=11×16
通过这样的分解,我们可以看到176有多个因数组合,每个因数都满足乘积为176的条件。
3
因数的组合。
,列举所有可能的因数组合,并说明其含义。
1:1×176
这个组合的意思是某个数乘以1等于176。这是数学中乘法的基本事实。
2.2×88
这个组合表示2和88相乘得到176。在现实生活中,这可能意味着两个人合作各得到88个人,合计176个人。
3.4×4
这个组合意味着4和44相乘等于176。这或许表示,在某个活动中,4个单元或个体各贡献了44个,最终达到了176个。
4.8×22
这个组合表示8和22相乘得到176。这可能表示在某些情况下,八个部分或单元每个部分贡献22,组成176的整体。
5.11×16
这个组合意味着11和16相乘得到176。这可能表明,在特定情况下,11个元素或个体各贡献16个,结果为176。
3
结论。
通过以上分析可知,176是由多个不同因数的组合得到的。这些组合不仅显示了乘法的多样性,也显示了数学在解决实际问题上的重要性。在日常生活中,我们会遇到各种各样需要用到乘法的情况,了解这些因数的组合,就能更好地理解数学知识,并运用它们。
3
就是发散思维。
除了这些因数的组合,还可以考虑以下几种方法。
1.如果我们只知道一个因数,怎么找到另一个因数?
2.在实际应用中,如何选择最佳因数组合来解决特定问题?
3.乘法在数学中处于怎样的地位?与其他数学运算(加法、减法、除法等)又有什么关系呢?
3
本论文通过探讨“什么乘以什么等于176”这一问题,不仅解决了这一问题,还对176的因数组合及其在实际生活中的应用进行了深入挖掘。通过这样的数学探索,可以更好地理解乘法的本质,在日常生活中运用数学知识解决实际问题。
